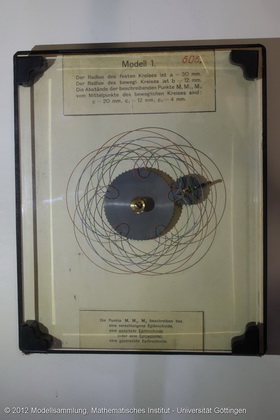
Kinematische Erzeugung der Epitrochoiden

Epitrochoide sind Spezialfälle der sog. Epizykloiden. Diese sind Bahnkurven, die ein fest mit einem Kreis K verbundener Punkt beschreibt, wenn K außen auf einem anderen Kreis abrollt. Befindet sich der beobachtete Punkt $P$ außerhalb bzw. im Inneren des rollenden Kreises, so spricht man verschlungenen bzw. gestreckten Epitrochoiden. Diese treten auch in der Technik auf: Das Gehäuse eines Wankelmotors wird durch eine gestreckte Epitrochoide beschrieben.

Betrachtet man einen Punkt, der direkt auf dem abrollenden Kreis liegt, so spricht man von spitzen Epizykloiden.

Die Bahnpunkte können mit \[\begin{pmatrix}P_x\\P_y \end{pmatrix}(t)=\begin{pmatrix} (R+r)\cos\bigl(\frac rR t\bigr)- b\cos\bigl(\frac{R+r}{R}t\bigr)\\ \bigl(R+r\bigr)\sin\bigl(\frac rR t\bigr)- b\sin\bigl(\frac{R+r}{R}t\bigr) \end{pmatrix}\] berechnet werden. Dabei ist $r$ der Radius des rollenden Kreises, $R$ der Radius des festen Kreises und $b$ gibt an, ob sich der beobachtete Punkt $P$ innerhalb des Kreises ($b < r$), auf dem Rand des Kreises ($b = r$) oder außerhalb des Kreises ($b > r$) befindet. Für Epitrochoiden gilt also $b \neq r$.

Ein Diapositiv dieses Modells ist zu finden unter der Modellnummer 1414.

Text geschrieben von: Julia Bienert