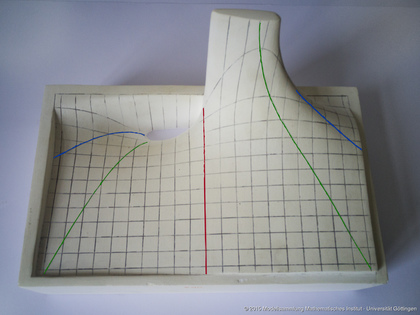
Wärmeleitung in einem Stab; Doppelquelle
Modell 290
| |
| Rubrik: |
| J 10 |
Beschreibung
Wärmeleitung in einem Stab. Doppelquelle. Orte der Extreme von t=const: grün. Orte der Wendepunkte von t=const: rot, blau. Gips.
Ergänzungen
Dieses Gipsmodell beschreibt eine Lösung der Wärmeleitungsgleichung, nämlich die Entwicklung der Temperatur in einem Stab, nachdem an seinen beiden Enden jeweils eine gegebene Temperatur eingestellt ist. Die Richtung t von hinten nach vorne ist die Zeit, und die Links-Rechts-Richtung $x$ ist die Position auf dem Stab. Zu jeder gegebenen Zeit, sind die Stellen extremer Temperatur in grün und die Wendepunkte in rot und blau eingefärbt. Die analytische Lösung ist $F_2(x,t)=\frac{x\cdot\exp(-x^2/4t)}{2t\sqrt t}.$
Zum Schaukasten des Modells Kasten Nummer 53
Literatur
Schilling, Martin(Hrg.): Catalog mathematischer Modelle, Leipzig(Verlag von Martin Schilling) 1911, 7.Auflage, Nr.364. S. 169.