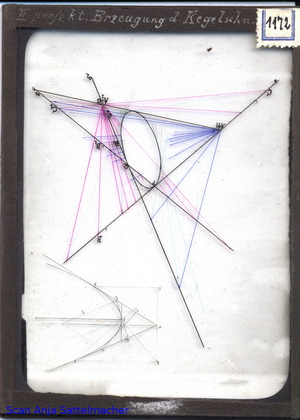
Diapositiv: Projektive Erzeugung des Kegelschnitts
Modell 1172
Beschreibung
Diapositiv: Projektive Erzeugung eines Kegelschnittes (Ellipse) durch projektive Punktreihen
Ergänzungen
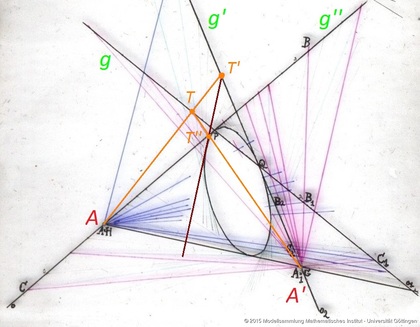
Die Geraden $o_2$ ($\hat{=}$ g') und $o$ ($\hat{=}$ g'') stehen in projektiver Beziehung und werden daher projektive Punktreihen genannt: Jedem Punkt T' von g' entspricht ein Punkt T'' von g'' (vgl. Bild 2).
Durch projektive Punktreihen lassen sich Kegelschnitte erzeugen: Verbindet man jeden Punkt T' von g' mit T'' von g'', so bilden die Verbindungslinien die Tangenten eines Kegelschnittes. Auch die Geraden g' und g'' gehören zu der Tangentenschar.
Die Erzeugung eines Kegelschnittes durch projektive Punktreihen ist dual zur Erzeugung durch projektive Strahlenbüschel (vgl. die Modelle 1170 und 1171).