2 ellipse drawers

The models under no. 544 are two elliptical compasses. These instruments consist of two perpendicular guide rails. On these rails a rod moves on two screws. In the first compass the rod is considerably longer and contains a drawing or marking device at the tip. By moving the rod, different half-axes can be adjusted. The second version of this model also contains two additional legs that are intended to serve as an extension of the rod to allow adjustments of larger half-axes.

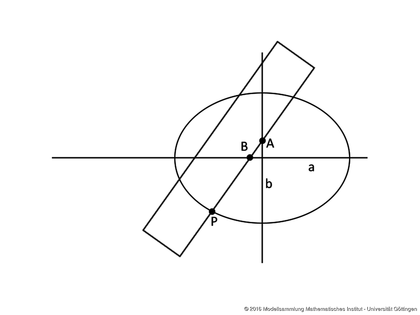
The functionality of these elliptical compasses is based on the paper strip construction of the second kind described below. The distance from the pin at point P to the first screw (point B) corresponds to distance b (small semi-axis of the ellipse) and the distance from the pin to the second screw (point A) corresponds to distance a (large semi-axis). The focal points of the ellipse are not important for this construction.

paper strip construction of the second type
In this construction variant, three points A, B and P are marked on a strip with dimensions $\overline{AP}=a$ (major semi-axis of the ellipse) and $\overline{BP}=b$ (minor semi-axis of the ellipse), where point P is not between A and B. If one moves the strip so that point B is on the major axis of the ellipse and A is on the minor axis of the ellipse, then point P moves on an ellipse. This construction is based on the following theorem.

If one end point and an inner point of a line segment move on mutually perpendicular straight lines, the other end point of the line segment describes an ellipse (see Picture 4).

Text written by: Elena Bachmann

Translated by: Laurent Bartholdi