Heat conduction in a stick; double source
Model 290
| |
| Category: |
| J 10 |
Description
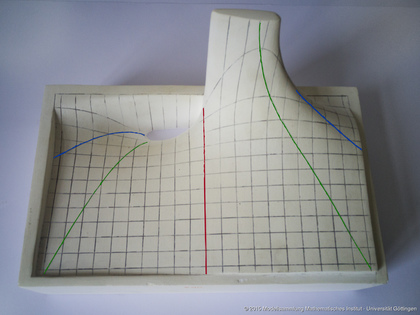
Heat conduction in a stick; double source. Places of the extrema of t = const: green. Places of the inflection points t=const: red, blue. Gypsum.
Additions
This plaster model describes a solution of the heat equation, namely the evolution of temperature in a stick after its two extremities are set to given temperatures. The back-front direction t is time, and the left-right direction $x$ is position on the stick. At any given time, the places of extremal temperature are in green, and the inflection points in red and blue. The analytical solution is $F_2(x,t)=\frac{x\cdot\exp(-x^2/4t)}{2t\sqrt t}.$
Showcase of this model is Case number 53
References
Schilling, Martin(Hrg.): Catalog mathematischer Modelle, Leipzig(Verlag von Martin Schilling) 1911, 7.Auflage, No.364. p. 169.